The understanding of the solar elevation is important in proper designing of the photovoltaic system and solar thermal system. The tilt angle of solar panels is decided based on the elevation of the sun in the sky.
Solar elevation angle calculator
Select the date & time and your timezone, enter your longitude & latitude to calculate the solar elevation angle (or solar latitude angle) and zenith angle. If you’re having trouble resetting the calculator, update it with your new metrics, then choose a different time zone then switch it back to the one you want.
What is solar elevation?
The solar elevation is the angular distance between the imaginary horizontal plane on which you are standing and the sun in the sky. It is also known as the solar latitude angle and measured in degrees. In simple words, it tells at what height the sun is in the sky. In the morning and evening, the sun is low in the sky, near the horizon. So, the solar elevation is close to 0°, whereas, at solar noon, the solar elevation angle is highest since the sun is overhead.

The solar elevation is the measurement of the height (or altitude) of the sun in the sky.
The sun rises from the east and reaches its maximum altitude at solar noon. Then, it descends to the west. Thus, the angle is always zero degrees at sunrise and sunset and maximum at solar noon. If the angle is negative, it means it is dark; the sun has either not yet risen or has transcended beyond the horizon.
Solar elevation formula
The solar elevation formula is as follows:
Here, ɑ is the solar elevation angle, δ is the declination angle, ɸ is the latitude of your location, and h is the solar hour angle.
Therefore, we require three variables (latitude, declination, hour angle) to calculate the elevation of the sun.
Let’s one-by-one understand each of the three.
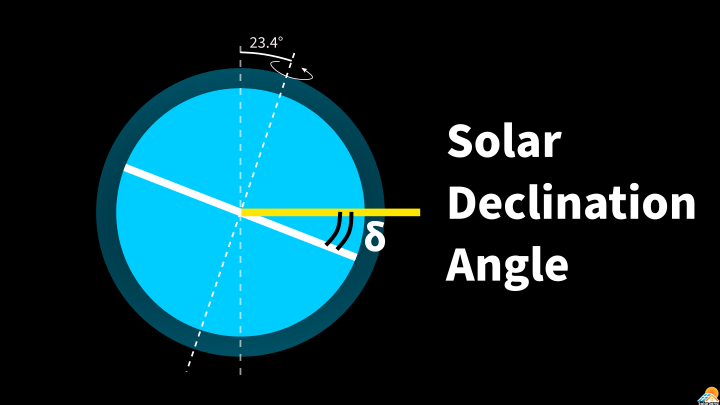
Declination angle
Our earth revolves around the sun in a particular orbit. Its axis of rotation is not perpendicular to the orbit as we might expect. Instead, the axis is slightly tilted by 23.44° from the assumed position. Because of this tilt, the earth’s equator always makes an angle to the sun’s rays, as depicted in the diagram below. This angle is the declination angle (δ).

The declination angle oscillates from −23.44° to 23.44° between the two solstices of the year. And it becomes zero at the two equinoxes (March 20th and September 22nd or 23rd).
The following equation enables to quickly calculate the declination angle:
Here, d is the number of days since the beginning of January 1st in UTC.
The above equation is not very accurate and often results in an error of one or two degrees. To find a better formula, follow this link: declination angle.
Latitude
The latitude of your location is the angular distance that measures how far you are from the equator. It is 0° at the equator and 90° at the poles.

The latitude (ɸ) is the angle between the earth’s equator and the line drawn from the center of the earth to your location.
You can find your latitude through Google Maps or any other standardized online map.
Solar hour angle
Solar hour angle is the measure of estimating the position of the sun relative to solar noon. By definition, it is 0° at solar noon. It increases by 15° after each hour and decreases by 15° before each hour from solar noon. Presuming solar noon at 12 o’clock, the solar hour angle will be +15° at 1:00 PM and −15° at 11:00 AM.
We can calculate the hour angle for any given time using the formula below.
Here, h is the solar hour angle, and LST is the local solar time in the 24-hour format.

The more accurate way to estimate the hour angle is available in the following article: solar hour angle.
How to calculate the solar elevation angle?
Knowing the formulae to calculate the declination angle and hour angle, we can determine the altitude of the sun for any location on the earth and for any time of year.
Let’s take the example of Tucson, Arizona. Tucson is at 32.22° latitude. We want to calculate the sun’s elevation angle at 10:00 AM, 12:00 noon, and 2:00 PM.
The solar hour angles at 10:00 AM will be 15°× (10−12) = −30°. Similarly, at 12:00 noon and 2:00 PM, the hour angles will be 0° and 30°, respectively.
Now, we need to calculate the declination angle for given times. We are interested in calculating solar elevation on March 3rd. So, d = 31+28+2 = 61 days. We can also account for hourly variations in the declination angle, but it will not significantly affect the result. Just for the learning purpose, we will calculate the declination angles for all three times.
At 10:00 AM, d = 61+10/24 = 61.4167 days.
In the same way, for 12:00 noon & 2:00 PM, d = 61.5 & 61.583 days and their respective declination angles are −7.81° & −7.78°. As mentioned earlier, the declination angle does not change significantly in a short period of time. We can see the values remain nearly constant.
Finally, we have all three declination angles and solar hour angles.
Thus, the solar elevation angle for 10:00 AM is as follows:
The elevation angles at 12:00 noon & 2:00 PM are 49.97° & 40.82°.
One point to observe over here is the solar elevation angles at 10:00 AM & 2:00 PM are almost equal. That is because the cosines of the hour angles (−30° & +30°) are the same. Therefore, the sun will nearly be at the same height in the sky at 10:00 AM and 2:00 PM.
A note to consider: In the above calculation, we have presumed solar noon at 12 o’clock, which may not be true. The calculator at the beginning of the article uses more accurate formulae, so the sun’s latitude will differ slightly.
Solar zenith angle formula
The zenith is the point in the sky directly above the observer, and the solar zenith angle is the angle between the sun and zenith with the observer. The zenith angle is maximum when the elevation angle is minimum. As a result, in the morning and evening, the zenith angle is highest, while at solar noon, it is minimum.

The solar zenith angle is complementary to the solar elevation angle. So, the addition of both always equals 90°.
Mathematically, the cosine of one equals the sine of the other. sin(θ) = cos(α). Using this, we can update our previous equation as:
In the example of Tucson, the zenith angles are 49.23°, 40.03°, and 49.18° for 10:00, 12:00, 14:00.
At equinoxes
The equinox is a time when the declination angle becomes zero. It happens twice a year, on March 20th and September 22nd (or 23rd). At an equinox, δ = 0°.
Substituting δ = 0°,
The solar hour angle is zero degrees at solar noon. So, the equation reduces to
Thus, at the solar noon on the equinoxes, the zenith angle equals the latitude.
Further, we know, on the equator, latitude equals zero degrees. So, at this time and circumstances, the zenith angle becomes zero degrees. It means the sun is directly above your head, and the altitude equals 90°.
Special timings
- At sunrise and sunset, the solar elevation angle equals 0°, and the solar zenith angle equals 90°.
- On the equator, a day of the equinox, the elevation angle equals 90°, and the zenith angle equals 0° at solar noon.
- In the day, the solar elevation angle and zenith angle are always between 0° and 90°.
- If the elevation is negative, it means it is dark.
Elevation and Zenith Plots
The graph below represents the variation of the solar elevation and zenith angles throughout the day. The date and place considered for plotting are March 3rd and Tucson, Arizona.

From the above figure, we can see the sun is at the highest elevation after 12:00 noon, around 12:30 PM. And the elevation angle is around 50°.
The plot below is the monthly variation in the elevation and zenith angles at Tucson, Arizona, 12:00 noon.

The monthly variation graph does not account for daily changes in the elevation angle.
As we see, Tucson receives the highest elevation in the months of June and July. It should be obvious since these are summer months in the northern hemisphere, and the sun is directly overhead in summer.
How to know the day with the highest or lowest solar elevation?
The elevation angle depends on numerous factors, including your latitude and longitude. Further, it varies hourly as well as monthly. The day on which the sun will be at the highest elevation will definitely be one of the summer days.
For people in the northern hemisphere, the solar elevation is highest on June 20th (or 21st). And for people in the southern hemisphere, the sun is highest in the sky on December 21st (or 22nd).
These dates swap in the case of the lowest elevation.
For people in the northern hemisphere, the solar elevation is lowest on December 21st (or 22nd). And for people in the southern hemisphere, the sun is the lowest in the sky on June 20th (or 21st).
The plot below gives the monthly variation of the elevation angle for Denver (39.74° N, 104.99° W) and Sydney (33.87° S, 151.21° E).

It is clear from the above chart, Denver, which is in the northern hemisphere, has the maximum elevation on June 20th (or 21st), whereas Sydney, which is in the southern hemisphere, has the maximum elevation on December 21st (or 22nd). The dates reverse for the lowest elevation.
Both curves in the figure are the same. The only difference is one is shifted by the number of days between the two dates.
Why these dates?
These are not random dates. They are the two solstices of the year. On solstices, we have either the longest day of the year or the shortest day. People living in the northern hemisphere will have the longest day in the June solstice and the shortest day in the December solstice. The reverse is true for the southern hemisphere.
Between 23.44° and −23.44° latitude
The previous charts become a bit strange if the region lies between 23.44° N and 23.44° S. This is the tropical portion of the earth—between the Tropic of Cancer and the Tropic of Capricorn. Here, the elevation peaks twice a year. The cause of such behavior is the declination angle.
In this region of the earth, the sun is at the zenith twice a year.
The graph below is for Macapa, Brazil (0.0356° N, 51.07° W).

Solar elevation and solar panels
The solar elevation is very important in deciding the inclination of solar panels, in both photovoltaics (PV) and thermal.
The maximum absorption of solar energy takes place when panels are perpendicular to the falling sun’s rays.

As we can see from the above figure, the surface of the panel is perpendicular to the sun’s rays. And basic geometry says it happens when panels are tilted at the zenith angle (θ)—or 90°−elevation angle.
FAQs
What is the sum of the zenith angle and solar elevation angle?
The sum of the zenith angle and elevation angle is 90°.
If I have a zenith angle of 11°, what would be the solar elevation angle?
The solar elevation angle and zenith angle are complementary angles, i.e., the addition of both equals 90°. So, the elevation = 90°−11° = 79°.
At what time of day the solar elevation angle is minimum?
The solar elevation angle is minimum in the morning and evening.
What is the difference between solar declination, zenith angle, and solar elevation angle?
The solar declination is the angle between the earth’s equator and the sun’s rays. The zenith angle is the angle between the zenith and the sun with the observer. And the elevation angle is the angle between the sun’s rays and the imaginary horizontal panel on which the observer is standing.
What would be the zenith angle if the solar elevation angle is 38.5°?
The addition of both angles equals 90°, so the zenith angle = 90°−38.5° = 51.5°.
How solar panels and the elevation angle of the sun are related?
To maximize solar power, we should tilt our solar panels at an angle equal to 90°−elevation angle.
On what days of the year is the solar elevation angle at noon, the equator is greatest?
The solar elevation angle reaches the highest, equal to 90° at the equinoxes, noon on the equator. The two equinoxes are March 20th and September 22nd (or 23rd).